[ recurrence relations , generating functions ]

Problem 26 : Number of Triangulations of an n-gon

This is a problem that is likely to resonate with everyone who ever sat for an aptitude test. I remember trying hard to keep track of all the triangles in a pentagon to find the number of triangulations. Well, there is a pretty general way of dealing with this! We can develop a simple reccurence solution for the same.

Let us start by drawing out a random n-sided polygon with numbered vertices a random diagonal.

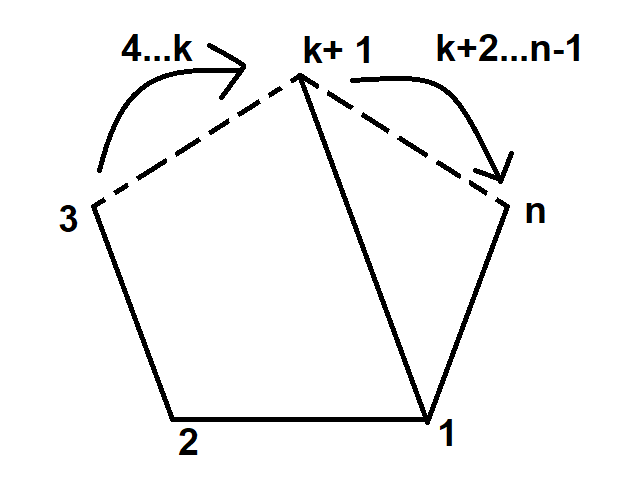
A random n-gon where dotted lines indicate that there are other vertices that have been skipped

Developing the recurrence

The diagonal splits the entire n-sided polygon into two sub-polygons - k+1 and n-k sided polygons. Let us denote the number of triangulations of an n-sided polygon as \(t_n\). Then, we know that the number of triangulations of the k+1 sided sub-polygon and the n-k sided sub-polygon will contribute to the total number of triangulations of the n-sided polygon. This leads us one step closer to a recurrence that will definitely contain the term \(t_{k+1}.t_{n-k}\). Note that we took a product of the two so that we can make sure we count all possible combinations of the triangulations.

Recurrence Relation

What do you do with that \(k\) there ? Naturally, we want all possible triangulations so we would simply sum over all valid k. In other words, the following equation holds

\(t_n = \sum_{k=1}^{k=n} t_{k+1}.t_{n-k}\) with \(t_1 = 0, t_2 = 1, t_3 = 1\). \(t_2\) was defined for the sake of setting up the recurrence properly. One can imagine joining the an open two sided angle to form a triangle.

Let us define a function -

\[f(x) = \sum_1^{\infty} t_n x^n\]

Then,

\[f(x) = x^2 + \sum_3^{\infty} t_n x^n = x^2 + \frac{1}{x}\sum_{n=3}^{\infty} \left(\sum_{k=1}^{n} t_{k+1}.t_{n-k} \right) x^{n+1}\] \[\implies x.f(x) = x^3 + \sum_{n=3}^{\infty} \left(\sum_{k=1}^{n} t_{k+1}.t_{n-k} \right) x^{n-k}.x^{k+1}\]

Since \(t_1 = 0, t_2 = 1\) we can write, \(\implies x.f(x) = x^3 + \sum_{n=1}^{\infty} \left(\sum_{k=1}^{n} t_{k+1}.t_{n-k} \right) x^{n-k}.x^{k+1}\)

Now, the second term on the RHS is essentially accounting for all the terms in the product of \(f(x)\) with itself!

So, we can write, \(\implies x.f(x) = x^3 + f(x)^2\) Using the quadratic formula to solve for \(f(x)\) we get, \(\implies f(x) = x\frac{1-\sqrt{1-4x}}{2}\)

Reminder : By definition, the coefficients in the expansion of \(f(x)\) represent the series of \({t_n}\). So, we’re basically done!

Binomial Expansion

The binomial expansion of \(\sqrt{1-4x}\) is given by,

\(\sqrt{1-4x} = 1 + \sum_{p = 1}^{\infty}\frac{(-1)^{p-1}}{p.2^{2p-1}}{2p-2 \choose p-1}(-4x)^p\) \(\implies \sqrt{1-4x} = 1 - \sum_{p = 1}^{\infty}\frac{2}{p}{2p-2 \choose p-1}.x^p\)

Finding \(t_p\)

Using the Binomial Expansion in the expression for \(f(x)\) gives us,

\[f(x) = \frac{1}{p}{2p-2 \choose p-1}x^{p+1}\]

So, we have our answer !

\(t_p = \frac{1}{p-1}{2p-4 \choose p-2}\)