Problem 4 : A Problem in Triangle Goemetry

This is one of those problem’s that’s close to my heart. I had encountered a similar problem during my High School days. This problem involving a triangle seemed simple at first (very similar to an old sibling-problem) and that’s just what caught me in a loop of attempts. Finally, I was able to come up with a very different approach The good thing about goemetry problems is that they are can be visualized. The triangle ABC is an isosceles triangle with base angle of \(80^{\circ}\). We need to find the angle denoted by a “?”.

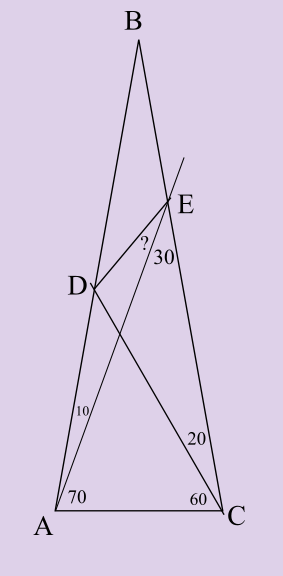
A Good Look followed by some Construction

Well, so we need to notice a few things here. First, the apex angle of the triangle is \(20 ^{\circ}\) which automatically makes the \(\Delta CDB\) an isosceles triangle. So, we want to make sure we use that property. Also, not that the base angle EAB \(= 70^{\circ}\) which means we can split it into \(60^{\circ} + 10 ^{\circ}\) and \(10^{\circ}\) compliments the base angles \(80^{\circ}\). So, let us go ahead and draw a right angled \(\Delta AGB\). Everything is constructed below (Sorry for the absence of padding).

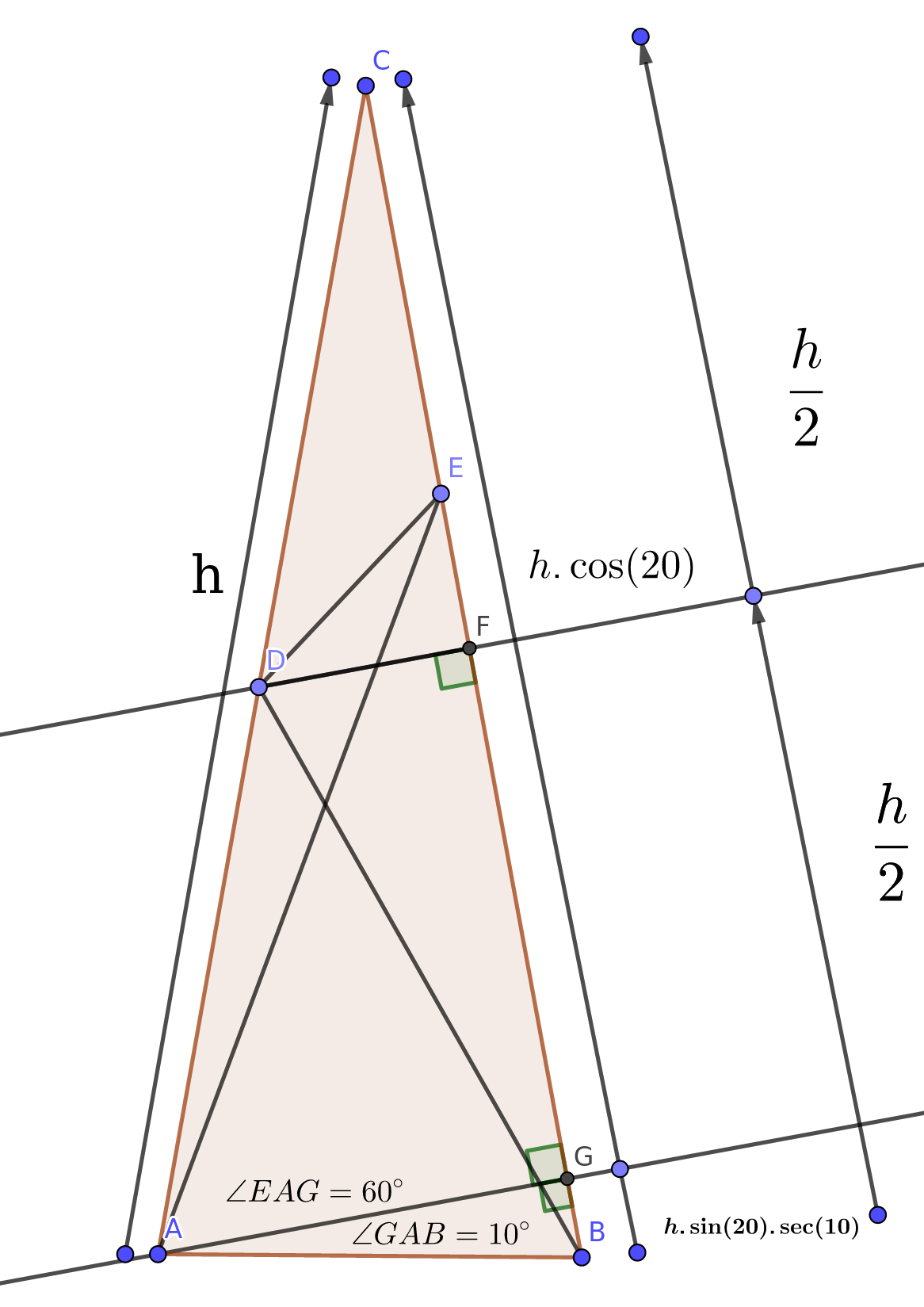
The Solution

The solutions is pretty straightforward from here. We label the length \(AC = CB = h\). Clearly, DF is the perpendicular of the isosceles \(\Delta CDB\) it will bisect \(CB\). This implies that \(CF = FB = \frac{h}{2}\). It is easy to note from the \(\Delta CAG\) that \(AG = h.sin(20)\) so, \(EG = h.sin(20).tan(60)\). Finally, from the right \(\Delta CDF\), \(DF = \frac{h.tan(20)}{2}\). This means, \(EF = CF - (CG - EG) = \frac{h}{2} - (h.cos(20) - h.sin(20).tan(60)\)

And here we go - In \(\Delta DEF\) : \(tan(\theta + 30) = \frac{DF}{EF}\) \(= \frac{h.tan(20)}{h-2(h.cos(20) - h.sin(20).\sqrt{3} }\)

Now go ahead and solve for theta using trigonometric identities (or a calculator).

Hint : Use \(cos(3\theta) = 4.cos(\theta)^3 - 3.cos(\theta)\)